世界原来都是弯曲的，黎曼带你重新认识这个世 - 缔客世界杂志社投稿

一、来稿必须是作者独立取得的原创性学术研究成果，来稿的文字复制比（相似度或重复率）必须低于用稿标准，引用部分文字的要在参考文献中注明；署名和作者单位无误，未曾以任何形式用任何文种在国内外公开发表过；未一稿多投。二、来稿除文中特别加以标注和致谢之外，不侵犯任何版权或损害第三方的任何其他权利。如果20天后未收到本刊的录用通知，可自行处理(双方另有约定的除外)。三、来稿经审阅通过，编辑部会将修改意见反馈给您，您应在收到通知7天内提交修改稿。作者享有引用和复制该文的权利及著作权法的其它权利。四、一般来说，4500字（电脑WORD统计，图表另计）以下的文章，不能说清问题，很难保证学术质量，本刊恕不受理。五、论文格式及要素：标题、作者、工作单位全称(院系处室)、摘要、关键词、正文、注释、参考文献(遵从国家标准：GB\T7714-2005，点击查看参考文献格式示例)、作者简介(100字内)、联系方式(通信地址、邮编、电话、电子信箱)。六、处理流程：（1）通过电子邮件将稿件发到我刊唯一投稿信箱（2）我刊初审周期为2－3个工作日，请在投稿3天后查看您的邮箱，收阅我们的审稿回复或用稿通知；若30天内没有收到我们的回复，稿件可自行处理。（3）按用稿通知上的要求办理相关手续后，稿件将进入出版程序。（4）杂志出刊后，我们会按照您提供的地址免费奉寄样刊。七、凡向文教资料杂志社投稿者均被视为接受如下声明：（1）稿件必须是作者本人独立完成的，属原创作品（包括翻译），杜绝抄袭行为，严禁学术腐败现象，严格学术不端检测，如发现系抄袭作品并由此引起的一切责任均由作者本人承担，本刊不承担任何民事连带责任。（2）本刊发表的所有文章，除另有说明外，只代表作者本人的观点，不代表本刊观点。由此引发的任何纠纷和争议本刊不受任何牵连。（3）本刊拥有自主编辑权，但仅限于不违背作者原意的技术性调整。如必须进行重大改动的，编辑部有义务告知作者，或由作者授权编辑修改，或提出意见由作者自己修改。（4）作品在《文教资料》发表后，作者同意其电子版同时发布在文教资料杂志社官方网上。（5）作者同意将其拥有的对其论文的汇编权、翻译权、印刷版和电子版的复制权、网络传播权、发行权等权利在世界范围内无限期转让给《文教资料》杂志社。本刊在与国内外文献数据库或检索系统进行交流合作时，不再征询作者意见，并且不再支付稿酬。九、特别欢迎用电子文档投稿，或邮寄编辑部,勿邮寄私人，以免延误稿件处理时间。

世界原来都是弯曲的，黎曼带你重新认识这个世

作者:

关键词:

摘要：

1854年，德国数学家伯恩哈德·黎曼（GeorgFriedrichBernhardRiemann）又发布了一篇与众不同的论文《论作为几何学基础的假设》。这篇论文给我们带来了一个全新的，遍地都是曲线的世界，这个世界再也不是横平竖直的了。

黎曼，这位大师，认识他的人无不惊叹与他惊人的创造，几乎每次出手不是颠覆某个领域，就是横空创造出一个完全没有的数学理论。比如前面半句的例子，就像是黎曼猜想，他居然能用一个方程的零点分布情况去推算素数的在某个范围内的个数。后面半句的例子就是他一手打造的黎曼几何。

先说明一下，我们从很小就开始学习几何学，知道三角形内角和是180度，知道勾股定理等等。这些几何学知识跟我们的日常认知是符合的，因此学起来不太费事，现在我们知道了这种“传统几何”叫作欧几里得几何。

然而，在某些情况下，欧式几何却有点不太符合实际情况。

举个例子，欧式几何里说，直线的长度是无限的，假如我们现在站在地球表面，沿着赤道做一块黑板，在黑板与地面等高的位置画一条线，并一直连续下去。这条直线虽然长，但是终究会回到原点的，这样一来，直线的长度就不再是无限长的，而是有限的了。

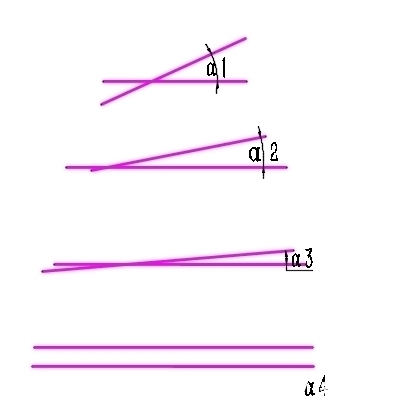
再比如，欧式几何中，两条平行线是没有交点的。但是我们现在来做个推论，如上图所示，α1>α2>α3，显然这3组线最终相交的点会越来越偏离图中心的，假如我们现在把两组线进一步偏移，使得α4变得无穷小，那么第4组的两条直线相交点就将无限偏离图中心的，既然你都无限偏离图中心点的，我们可不可以认为这是平行的呢？在这个问题上，黎曼几何认为，在同一个平面上任意两条直线总是会相交的，也就是说不存在平行线。

人们很快意识到，黎曼的这种新几何与人类探讨了几千年的欧式几何并没有本质的区别。黎曼也是从最简单的几条公理出发，继而推导出了完备的理论体系，在这个体系中，所以经过严密论证的论题都能完美自洽，不存在不能自圆其说的情况。

那么黎曼几何到底有啥用呢？我们再来做个不太恰当的比喻，有一只蚂蚁在一只皮球上爬，它不停地努力去爬，结果却发现它所接触的表面怎么也看不到尽头。如果这只蚂蚁没有好好去思考，那么它将永远被困在这个皮球的表面，早晚得崩溃。假设这是只聪明的蚂蚁，它了解一点黎曼几何的原理，它便可以在不脱离这个球体表面的情况下，意识到脚下的球面其实是有弯曲的。如果它再懂得更多一点，它甚至能算出来自己走了多少弧度，长度，面积，正因为脚下的是球面，所以当然可以从一个点出发走下去之后，回到出发点。当它意识到这个问题时，这只皮球便再也困不住这只蚂蚁宏伟的思想了。一瞬间，这只蚂蚁便超过了它所在的维度了。

假如我们就是这只蚂蚁呢？我们现在好像也觉得宇宙是无边无际的，如果我们可以像那只蚂蚁一样，可以突破自己所在的维度来思考问题，那么别看现在动不动距离地球多少亿光年的星系，其实在更高维度上，我们都是瞬间到达的。

好了，以上举的那只蚂蚁的例子是晓然菌的空想主义，不过意思差不太多。在黎曼几何诞生过半个多世纪后，在物理学界找到一个量身定制的应用。爱因斯坦在推导广义相对论场效应方程时，遇到不少困境，后来有朋友把黎曼几何的理论介绍给他，结果爱因斯坦惊讶地发现，黎曼几何的很多假设和结论跟广义相对论的核心内容不谋而合。比如，爱因斯坦认为我们的时空其实是弯曲的，尤其在大质量天体附近弯曲程度更加严重；时间只是在小范围内存在着近似均匀，而这一小范围的近似均匀就是我们熟知的欧式几何。

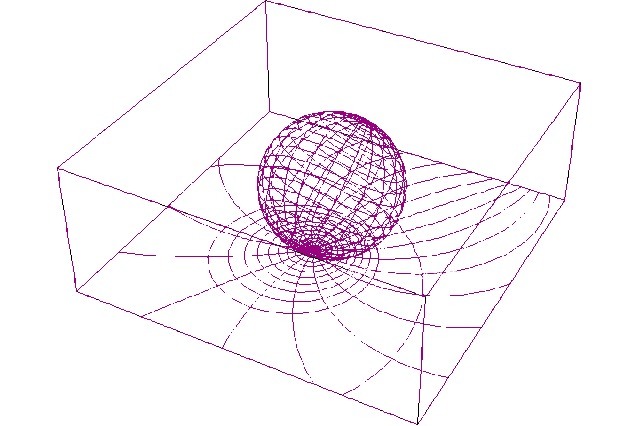
原来爱因斯坦遇到的困难，数学上的工具早在半个多世纪前就已经建立好了。

黎曼大师真是一出手就画出了最灿烂的数学篇章。

文章来源：《缔客世界》网址: http://www.dksjzz.cn/zonghexinwen/2021/0226/518.html